Original: NS = S - BD = I – TD
The expanded community there is no Trade Deficit (TD), but there can be a Government Budget Deficit (BD). This means that the National Savings (NS) is the combination of the US community and the off-shored (expanded) community. This same combination argument can be applied to Savings (S) and Investments (I).
I'm going to add a simple production function F(i(1), i(2), ..., i(m)) and use the concave rule:
if f(x) > f(x'), then f(yx + (1 – y)x') > yf(x) + (1 – y)f(x') for any y E (0, 1).
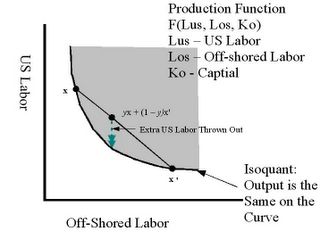
In words; The output (GDP) of the US community [f(x)] is greater than the output (GDP) of the off-shored (expanded) community[f(x')]. Therefore the weighted combination of the two “communities” is inside the isoquant of the production function. This is economically inefficient. To bring it back onto the isoquant (technology efficient) and therefore make it economic efficient, one needs to add a condition of throwing away the extra input. I'm going to say that this thrown away part is the US output, hence it is the US's community's “trade gap”. See figure 1.
I'm giving the US community and the off-shored (expanded) community a progressive tax system. There is no tax revenue sharing between the two communities implies that a part of the off-shored (expanded) community's tax is paid by the US community without a reciprocal payment. This implies that the thrown away input is not counted. Therefore, the US trade deficit and the US government debt are in fact twins.
Off-shoring/illegal alien employment is labor arbitrage. I'm going with this definition of arbitrage; is the practice of taking advantage of a state of imbalance between two (or possibly more) markets: a combination of matching deals are struck that exploit the imbalance, the profit being the difference between the market prices.
The effective labor is more like a range. Think of it as a curve drawn with a marker rather than a thin pen. Equation 4 is the familiar returns to scale with arbitrage inputs, in this case labor. Equation 2 is a constraint on labor employment and equation 4c is the constraint when a input change is needed. It is obvious that the scale operator is NOT a linear operator. The same procedure can be used to generalize the production function to include any arbitrage input. Also, Multiply outputs can be casted into a constraint equation.
Equation 2 reflects the need to account for two real world developments.
- It needs to account for investing in a command economy, like China. Command economies place price controls on goods and services. This is harmful during times of inflation, with respect to a market economy. Expectation of yield is eroded, hence, margin of capital decreases. Under such circumstances it is prudent to remove one self from that market to lower ones risk. However, if one wants to maintain a presents in that country, like China, for the exposure to over 1 billion consumers then economic efficiency is NOT a driving force.
- The ease of goods, services and people to cross borders has made a technique of production decision not as “final”. “Putty-Clay” model is not a valid model in some economic sectors. Examples: call centers and software development, in general, any thing that can be encoded into a data stream is no long subject to cost of change.
More on these two ideals later.
The arbitrage of labor is a measure of how one labor market can be substituted for another labor market. The elasticity of scale or elasticity of production measures the responsiveness of output to an increase in all inputs by a scale factor. Elasticity of scale applied to arbitrage labor inputs does not give any clue as to how the various labor inputs can change. Elasticity of substitution measures the percent change in factor proportions due to a change in marginal rate of technical substitution. This concept can be applied arbitrage inputs. The output is the effective labor force.
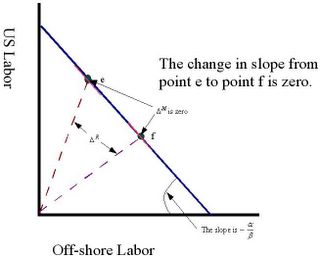
Case 1 – Perfect Substitution
The isoquant is a straight line and the curvature along any point is the same. The elasticity of substitution is infinite. See Figure 1.
There is no free ride in economics. There is some sort of cost associated with labor arbitrage. Some examples can be a dialect difference that annoys callers or some sort of quality control issue.
The output of labor function (equation 2) is a constraint of two variables which limits how those two variables can be distributed. Imagine a cube 1 unit by 1 unit by 1 unit and a box of length by height by width. Fill the box with a random number of black and white cubes. The box can be filled with all black cubes at one time and all white cubes at another. In general, the box is filled with a different number of white and black cubes. Assume that adding a cube is not related to the color of the previous cube. Also, assume that filling the box is not related to any previous filling of the box. One can expect that the probability of black(white) cubes will follow the normal distribution (bell) curve.
The filling of the box concept has two important assumptions:
- The number of black/white cubes is finite. This describes a collectively exhaustive system.
- The box can only be in one “filled” state. This describes a mutually exhaustive system.
Suppose one constrains the number of black cubes. The probability distribution for the black(white) cube will be skewed. In general, the number of whites cubes is not depended on the number of black cubes. The number of white cubes does not equal the difference between the total number of cubes in the box and the black cubes. This concept follows the basic definition of Neoclassical theory, factor prices and quantities employed are determined simultaneously by the supply and demand for factors. In this case, the supply and demand for domestic and offshore labors.
Basic Labor Arbitrage Law:
Reward using Labor from Market A = The Disincentive of using Labor from Market B.
The nature of the reward is based on the context of the analysis.
Basic axiom: The distribution of labor for a given economic sector is a response the producer desires to achieve the maximum reward. The end result is a skewed distribution density for each of the arbitrage labor inputs.
The probability density of the sum is the convolution of the probability density of each of the labor input.
One needs to calculate a future state from the current state. This can be done using a matrix of transition probabilities.
Another look at Perfect Substitution.
The straight line indicates that there is no penalty in going from a state L(1) to L(2). This implies that the probability of transferring one labor at state i is at least the same as transferring one labor at state j.
A note on diminishing of returns: It is not conceivable the senior management and the board of directors will remove themselves for the good of the shareholders. In effect, this transition will result in a high cost and is can be said to be diminishing of returns.
The Producer's matrix of Transition Probabilities (PTP).
The producer's matrix of transition probabilities is a regular stochastic matrix. The producer's matrix of transition probabilities has a steady-state (equilibrium) probability vector such that :
The producer's matrix of transition probabilities is, in this case, a hidden Markov model. In other words, one does not have knowledge of the actual probabilities, but one does have the model.
The Intensive Production Function and the Producer's matrix of Transition Probabilities.
The output-labor ratio is defined to be Y/L, however, L is now related to a probability density. L can be calculate by adding the expectation values, but this technique gives no information as to why there is a shift in one labor market over the other. The shift of the capital – labor ratio k = K / L can be interpreted as the likelihood that a change from k to k' takes place.
A side note about US corporations investing in China, income distribution and the "Fisherian" approach:
“If we see movements in macro variables like aggregate output, the price level, or interest rates, then one of the following must be the cause:
(1) there is a real change, i.e. people's preferences, technology and/or endowments have changed, and all that we are observing is merely a change in equilibrium. The fluctuation is not a "crisis" at all, but actually an efficient response.
(2) money has changed and price levels fluctuate, but the "real" economy has not changed at all. The fluctuation is only nominal or "illusory". This is not a "crisis", merely an inconvenience.
(3) there has been a monetary change as in (2) but, because of sluggish or uncoordinated price adjustments, it has thrown all real prices into confusion and led to wrong signals and misallocations. This is a "crisis", but it is only temporary.
(4) there has been a real change as in (1), but for some reason or another (e.g. labor unions, etc.), there are institutional rigidities that prevent real prices from adjusting to the new equilibrium. This is a serious "crisis" that may last for a long time unless (or until) the institutional rigidities are removed.”
Investing in China can be seen as an “institutional rigidities”.
Neoclassical theory on the distribution of income. The labors get wL and the capitalists get rK where L units of labor employed in the economy, each unit paid a wage w. The income of labors is wL. If K units of (fixed, endowed) capital are employed and payed a return r, then the income of capitalist is rK. The distribution of income is how the total output in the economy Y, is divided up among the people. S = Y – wL – rK where is the the “surplus”. The “surplus” has two forms depending on the entity that is getting the surplus.
The economic surplus is the amount not paid out to factors in reward for “factor services”. It is determined by:
The entrepreneurs residual is the amount not paid out to the factors in reward for “factor services”. The difference between economic surplus and entrepreneurs residual can be looked as a bet made by the labor. The labor offered $X.00 for his/her service when he/she was willing to settle for $Y.00 ($X.00 > $Y.00). This is an opportunity cost for the entrepreneurs . The entrepreneurs residual is determined by:
The entrepreneurs' use of labor arbitrage has information that the labors in market A can use. The labors in market A are “NOT” competing against each other, they are in fact, competing against labors from market B. In the command economy of China, labors' wages are set and are therefore below those in the USA.
This has two effects;
- It forces wages below that a labor is willing to take.
- It lowers the entrepreneurs residual.
This effectively flattens out the the labor supply curve. Labor has become elastic (serfdom). Real wages RW = w / p (p is price) decreases and so does real output.
The command economy of China has also effected capital. The driving force is not the return of capital, but the return of investment.
Perfect substitution implies a return of capital. This can be understood using the concept of time. Assumed that labors from market A and market B have the same skill set. A's w is less than B's w. Cost from market A is C = (w, y) is less then that from B; C = (w',y). Introduce a change of capital k to k'. The return of capital is greater from market A than that from market B. Introduce a change of investment from i to i' that is set to return Q in a period t. Anything can happen in either market. One must have knowledge of the risk associated in investing for that time period. The preference for labor in market A over market B can be seen in the output per unit capital at the Bureau of Labor Statistics. See series MPU300002, MPU740022 and MPU750022.
A US corporation investing in China is a hope that they get a return from their investment in some future date. Currently, China is a investment sink with respect to a market economy.
In general, investing in a developing, market economy is a bet on future returns. It was shown that labor arbitrage has the effect of lowering incomes to a point were the US labor market for that sector shrinks.
The producer's matrix of transition probabilities has the effect of changing US and the off-shored labor densities. The long term application of the PTP, to a market economies, is to equilibrate the labor densities.
The PTP is a stochastic matrix with eigenvectors (base). The PTP changes the probability of a labor state over changing states. The effect of this application, to a labor density, is to produce a probability wave for any given labor number. The expectation value from the labor density follows a curve described by maximum probability move from state i to state j.
A Side Note: It is evident that this theory is not compatible with a some analysis like cost minimization and profit maximum theories (etc...). This theory is NOT an equilibrium theory. It is more like a “global social experiment” in progress (a non-equilibrium theory).
As note previous, labor arbitrage removes the “rental” wages from the entrepreneurs residual. The simplest consumption function is of the form C = cY where c is the marginal propensity to consume. Y is the “expanded” communities output. One can rewrite this to;
the above equation makes the simple saving equation:
the equilibrium equation I = S is not valid. This is a money flow problem. This can be shown using a simple 2 period income stream function. Households can lend present income to increase future consumption or borrow from future income to increase present consumption. Borrowing is a negative S.
The above equation can be rewritten as:
The situation is different for the next period.
In order to maintain a positive GDP, money has to “flow into the system”. The best way for money to flow into the system is to use that money, which is due to a lower price and reinvest into the system. This implies that at any given period, only the consumption of output from outside the system needs to be replaced. However, if the money comes from outside the system then it can be seen that at any given period, the savings at the start of that period is reduced by a multiple of the consumption of output from outside the system.
The duality of this problem is the behavior of the consumer and the propensity to consume.
It's a Matter of Degree, not of Hidden Variables
When a labor market is in direct competition with low wage labor markets there must be a way to mathematical describe the redistribution of incomes. One needs to look at the following paper: Hall - Separating the Business Cycle from Other Economic Fluctuations
There is this model called DPM (see above paper). This model treats the employment process as a call option. Hall attempts to satisfies the wage differential by applying a concept of sticky wages. In the section Producer's matrix of Transition Probabilities Revisited, I argued that in the case of perfect substitution, the multi-factor productivity is the driving force due to the greater return on capital. This is in direct contrast to Hall's view: "As long as productivity is high so is the employment level". The dollar's current weakness indicts that productivity is not the driving force. The weak dollar is indicating a negative sector growth (see Federal Reserve and Monetary Policy for details).
The alternative explanation due to Kennan is also wrong. He assumes that there are hidden variables. There are no hidden variables. A US worker knows that his wages and benefits are much higher than that of a low wage earner from China and India as an example. US labors are being replaced. The replacement of the US labor force is a matter of degree. This implies that the classical supply and demand for labor is not appropriate for the global work force. A better description follows;
Labors from market A and market B have knowledge of each other. Assume that labor cost from market B is much lower that labor cost from market A. The implication is reflected in the bounding of the market A's labor force. It is bounded below by a minimum wage and it is bounded above by the knowledge of the other market's labor force. Given an independent laborer in a sector from market A , computer programming for example, then one can say that his/her economic earnings are bounded by the minimum wage and that his/her rental earnings (plus economic earnings) become upper bound. This upper bound has, in effect, removed the infinity from the positive labor supply curve. If the laborer's rental earnings are too high, that laborer must come down in rental earnings.
Given these random variables (laborers earnings), one can construct a random probability density function that is independent from the other labor markets. This pdf is always there, exerting its influence, forcing real wages to decrease. The decrease in “rental” wages has manifested itself into the lower values of cars, planes, etc... (the value of the car, for example, is the price of the car). It is contributing the the never ending, increasing pressure on the US labor force to make ends meet. Heath care and pension plans are now under assault due to the lack of wage gains.
The Relation between the Value of Money and the Velocity of Money
In a very simple model one can see the relation between the velocity of money to its value (or more precisely its future value). The higher the velocity of money implies more money in the system, its value decreases, which in a free market means inflation. The reverse is deflation.
One must accept the following generalization;
velocity of money = change of money in the system / a period of time
The velocity of money implies that one can attach a “frequency of money”
Under certain conditions one can attach a “phase” to the value of money.
See Ergodic Theory for details.
The following are some central themes to “Monetarism”
(1) monetarist transmission mechanism: urging that agents dispose of excess money supply by purchasing goods rather than bonds.
(2) stability of money demand: belief that, in practice, the demand for money is a stable function of wealth, prices, price changes and interest.
(3) money-to-income causality: that movements in the money supply have been the primary cause of business fluctuations and that movements in aggregate demand for goods have relatively little impact.
(4) natural rate of unemployment hypothesis: belief that there exists a unique rate of unemployment that is associated with non-accelerating inflation and that, in the long run, the economy will settle at such an unemployment rate.
(5) superiority of monetary policy rules: assertion that monetary policy is much more effective than fiscal policy, recommendation that Central Banks target money aggregates rather than interest rates, and that following a steady money supply growth rule is, at least in the long run, better than a discretionary, counter-cyclical monetary policy.
Theme number 4 implies some sort of ergodic theory. See Ergodic Theory
Definition: In general the time average and space average may be different. But if the transformation is ergodic, and the measure is invariant, then the time mean is equal to the space mean almost everywhere.
The “time” and “phase” averages taken together, in a very simple model, implies that “Monetarism” is a study of “measure-preserving dynamical system”
See Wikipedia for the definition. I want one to focus on an example called “subshift of finite type”. Under simple cases, one can form a “topological Markov shift”. In other words, one can use Markov Chains to study dynamic systems.
This implies that my equation for Neoclassical Theory of Production has it's dual to “Monetarism”.
The convolution of probability densities can be made into a Quotient map. This implies that the “Keynesian” or a “Global Keynesian model” (convolution of probability densities) has topological properties.
In other words, this theory is a unification theory.
Transformations and Trade
The last section showed that there exists a topological space for global economic production. This topology assumes that all markets/countries have their own topological space/manifold. In the case of expanded communities or as Greenspan calls it “home bias”, has been removed, there exist a transformation that is due to the convolution of independent labor probability densities.
What needs to be discussed is the topic of trade or, in other words, specialization.
Basic axiom: Each market/country topological manifold represents the same object.
This axiom means that all econo-political-social topology spaces can be transformed into each other.
I will make the assertion that one can form a topological manifold that is diffeomorphism. This is the easy way out in showing the Trade aspect of globalization and its incorporation into the topology of global production.
Given the assumption that global topology is diffeomorphism, there exist pullback and push forward transformations between bases vectors of each topological manifold.
Given bases vectors for market A and bases vectors for market B, bases vectors transforms as (I'm not including the vector aspect in this):
In this case the bases vectors are the same, hence, the above will be a n x n matrix.
If the elements of the pullback (push forward) were related to cost, then the pullback (push forward) will be a representation of the real exchange rate of the bases vectors. I will use the tradable non-tradable definition of real exchange rate:
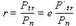

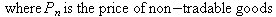
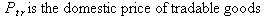
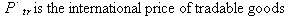
The pullback (push forward) bases transformation is a representation of the real exchange rate. The pullback (push forward) bases transformation merges the purchasing power and the trade, non-trade definitions of real exchange rate. This assumes the nominal exchange rate (e) is independent of the bases vectors.
One can look at the diagonal elements of the pullback (push forward) bases transformation as a representation of “the real exchange rate” of that bases vector element and the off diagonal elements as a some sort of technological change, if one exists. A good example of this is sugar into ethanol. If a bases vector includes oil and sugar then the pullback (push forward) bases transformation represents the change in cost of oil produced in market A over the change in cost of ethanol produced in market B and the other diagonal is the change of cost of oil produced in market B over the change in cost of ethanol produced in market A.
One can notice that the technological change of Neoclassical Theory of Production has been incorporated into trade, which itself is part the topological aspect of global production.
In general, one can get the real exchange rate by noting the following:

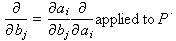

assuming e is constant.
Bad News – Good News
Bad News: Nominal Exchange Rate (e) is not a constant. It depends on many factors such as international debt, money supply, trade, etc.... This implies the components of the real exchange rate are components of a tensor made up of e(x1, y1, ..., xm, ym) convoluted with both domestic prices P(x1, ..., xn) and international prices P(y1, ..., yn).
Good News: Tensor Analysis and Differential Geometry can get one the real exchange rate. (I'm working on this. It takes time). This implies that there is a "Nominal Exchange Rate (call it the cost of living in a local region) between a country's local markets.
Independent Variables, Adam Smith and (Social)Stability
- The Free Hand of the Market
- Labor determines the price of commodities. I'm not going to use his cost of production as a starting point. Instead, I'm going to use "labor determines the price of commodities" by "us"consuming them.
I’m going to put these two themes on a mathematical foundation. I will like to start with independent variables. This is a simplified model. I'm not looking at final goods and services. My basic assumption is that these are linear combination of a fundamental base.
My first assertion, not a proof, is to state that there are NO hidden variables. Mankind has developed a sense of value to all that he uses. Value has been attached to pigs, sheep, wheat, corn, information and transportation (etc…). I will also assert that pigs, sheep (etc…) and wheat, corn (etc…) are independent and not a linear combination of husbandry and agriculture, respectively. In general, computers, etc.. are linear combinations. It makes the overall discussion of topological spaces easier. However, if ET should land and want to trade corn for some of his/hers/it’s fruit(?) then one can see that an unknown addition to the agriculture(?) varbles has shown itself. ET's space drive is a linear combination. I will defer this discussion until the time ET does land.
One can describe the concept of “Labor determines the price of commodities” by using a Discrete Markov Chain.
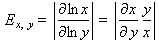

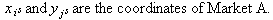
The free hand of the market, elastic and inelastic commodities can be incorporated by selecting the properties of the transitional matrix.
- In general, elastic commodities exhibit cycles whether they are seasonal or occur over generations. This implies that the transition matrix be Periodic. A process is periodic if there exists at least one state to which the process will continually return with a fixed time period (greater than one).
- Reality has shown that history repeats itself. This implies that the transition matrix be Positive Recurrent. Positive recurrent means that the expected return time is finite for every state.
- In general, inelastic commodities occur because of a supply shortage and/or no viable substitute can be found at a given price. Inelastic commodities can be transformed into elastic commodities by finding a new source and/or a new process can be applied. This implies that transition matrix is not irreducible. Irreducible means that every state is accessible from every other state. I will assume the state space (vectors) may be partitioned into a set of (irreducible) communicating classes, each of which may be classified as above.
One can now argue the question: “What is the topological space that describes a stable society”? If there is a topological space that represents stability then there exists a process that moves this topological space. If a society wants to be in state I, but is in state J, then there also exists a process that moves the topological space back toward stability. (Newton’s Law: for ever action there is an opposite and equal reaction) It can be shown that neither the existence nor the uniqueness of a stationary distribution is guaranteed for the above transition matrix C. Reality gives us a way out of this mess.
Some definitions:
Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written P(AB), and is read "the probability of A, given B".
Joint probability is the probability of two events in conjunction. That is, it is the probability of both events together. The joint probability of A and B is written as P(A,B).
Marginal probability is the probability of one event, regardless of the other event. Marginal probability is obtained by summing (or integrating, more generally) the joint probability over the un-required event. This is called marginalization. The marginal probability of A is written P(A), and the marginal probability of B is written P(B).
Note that there need not be a causal or temporal relation between A and B. A may precede B, or vice versa, or they may happen at the same time. A may cause B, or vice versa, or they may have no causal relation at all.
My definition of a “Market”, it is a marginal process.
Using my definition of “markets” means the Consumer’s transitional matrix can be constructed with joint probabilities. This allows a new source of an inelastic commodity to be “found”. The condition of not irreducible can be lifted.
The use of joint probabilities gives the freedom to introduce other states not controlled by labor/consumer. A new discrete Markov process can be shown to exists that uses the Chapman-Kolmogorov equation:
P(t + s) = P(t)P(s)
Other states are due to governments and corporations. Classification (irreducible) of the labor/consumer transition matrix is a problem, again.
Nothing has been said as to the mechanism that transfers the value of one bases to another. The simplest is a reciprocity system.
Fundamental-Markets, Storage and the Division of Labor
I'm going to call my definition of a market (a marginalization process) as the "fundamental-market". My construct of the Labor/Consumer transition matrix is periodic and the function of markets is to transform inelastic commodities into elastic ones. This very nature means that elastic commodities remain elastic. The fundamental-market has no distribution of “wealth” problems. The fundamental-market is continuously striving toward elastic commodities. Society is stable. We all live like kings and starve like paupers. There is no reason to blame any one person. Hunters and Gathers population are controlled by the land just as any other animal population. “We” are smarter(?). “We” developed a means of storage (ok, “we” infringed on the squirrel's patent).
Storage is also a marginalization process. It can be controlled by societies (governments) or individuals (companies). There is a problem if an individual does their own storage. It takes time and space. Storage is a process that screams division of labor. Division of Labor and the Distribution of “wealth” problem goes hand in hand.
P(Storage) = P(societies(?) (+ companies)(?))
P(producers + societies + companies) = P(producers)P(societies)P(companies)
Let's assume that society controls storage (for the good of society). In this case there is no stress on society except the usual Uglug is not doing his part. Society, as a whole, is stable and the Labor/Consumer transition matrix is irreducible and no longer periodic. The system has an unique stationary state.
Individuals (companies) controlled of storage can destabilize society. One way of achieving this state is not releasing the commodity when there is a shortage. The fundamental-market can no longer function and an elastic commodity becomes inelastic. The Labor/Consumer transition matrix is not irreducible, however, its also no longer periodic. There is no unique stationary state and the stress on society depends on were the stationary state lies.
Consumption is a marginalization process.
Axiom: The transition matrix of a society is P(Society). Society is defined as a group of individuals plus their form of government.
P(Society) = P(Consumption + Production + Storage)
P(Consumption + Production + Storage) = P(Consumption)P(Production) P(Storage)
Notice: there is no “money” exchanging hands yet societies can go into stress. Money is NOT the root of all evil.
Commodity monies are representation of commodities. The quantity of each commodity money increases, over time, due to the action of the fundamental-market. The quantity of a commodity money may or may not change the value of any one commodity.
In general, what is money?
Before I discus money I need to describe the vector space and what does the transition matrix represent. This will allow me to explain what I'm marginalizing.
Side Notes:
My axiom [P(Society)] does not guarantee the exists of a stationary state. The consequence of this can manifest itself when one tries to “neutralize risk”. Long Term Capital Management's mistake was that they assumed the global economy was a Brownian Motion (my opinion, no proof). “Neutral Risk” implies that the current stationary state is at or close to the stable state.
Fiat money and commodity money living side by side is a big mistake. The “Dot Com fiasco” was stocks (commodity money/funny money) being used to buy assets. G.W. Bush's economic plan is to use the housing boom (land that produces no output) to buy assets (land that produces output) from other countries.
This is were I part from Adam Smith's "cost of production".
Elasticity is defined as:
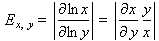
Diffeomorphism on the manifold assumes each market is the same object. Example: Market A is a tea cup and Market B is the donut. Market A and Market B can be the same market that has undergone a transformation. Elasticity can be defined under a coordinate change as: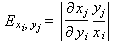
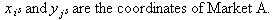
Let's assume there exists tangent/co-tangent bundles. I will assert that there is an equivalence class (C(-1) - C(alpha) structure, Taylor polynomials about a point and the Jacobian exists). I will also assert the Quotient Space (formed by this equivalence class is separated
(T(2)). This requirement identifies each commodities' value (the value of corn is different than the value of sugar, etc..).
Linear combinations are either topologically distinguishable or they can be distinct.
The motivation for the above construct is the realization that “price” is relative. Lagrangian densities, in field theory, are polynomial forms relative to velocities. If one is in quantum field theory there is the Hamiltonian formalism. The above construct allows one to use a 2-jet without any problems of missing properties. See Jet at Wikpedia for 2-jet under a coordinate transformation.
The only thing I what to point out is the exists of an acceleration term in the 2-jet that implies a “force” is present if this term is not zero. The vector space of the Chapman-Kolmogorov Markov process, of which my axiom's P(Society) is the transition matrix, can be described by the Fokker-Plank equation with stochastic forces (see Wikpedia: Fokker-Plank).
It should be noted the concept of labor and consumers are independent from the concept of “people”. The equivalence class/guage is invariant with respect toward who(m) is(are) doing the production and who(m) is(are) doing the consumption. This concept should not be hard to image. Horses, oxen and robots are placed in production roles. These entities are also placed in the consumption role. Neoclassical theory uses the concept of “labor” intensive vs. “capital” intensive processes. In general, capital (corn, wheat, gold, etc..) and labor (people, horses, oxen, etc..) are duals to each other. Example: one can describe an inductor using current flow. The same device can be described using the magnetic field.
Therefore, I will state my convention as the following:
- Capital belongs to the “vector” space.
- Labor belongs to the “co-vector” space.

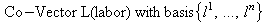
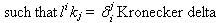
Example: Cobb-Douglas production function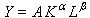
is a multiplication of “vector” (K) with “co-vector “(L).
It should be obvious, Labor (co-vector space) is an abstraction (useful math tool) of “people, oxen, horses, robots, ...”.
One more example. A push-forward of Output Y = f(x1, ..., xn) is the total derivative of Y at p. Neoclassical theory assumes the first partial derivatives of Y, at p, are greater than or equal to 0 and the second partial derivatives, at p, are less than 0.
- When does capital become labor?
- What becomes of the return to scale? Neoclassic theory like the constant 1/L.
- Prices are relative with respect to markets. Where does the velocity of money come into play? (prices are relative in time: inflation, deflation)
- What does storage do and how can it generate “wealth”?
- Real world uses labor and capital from different markets. How does this change the output equation and what is productivity?
Stochastic Processes and Dynamic Programming
I will begin this simple model by assuming one person has X amount of value to buy and others has Y(i)'s amounts of value to sell. I will not specify as to their relative amount of X and Y(i)'s.
The buyer's needs are: wood and/or coal for heating/cooking
corn and/or wheat and/or soybean for eating (they're vegetarians)
I will assume that there is a seller for each of these items.
The motivation for the buyers' state is to get a form of consumer utilities-maximization function (C1, ..., Cn steps).
Definition: buyer's unit of usage is the quality of a category he/she uses in one day.
Buyer's states:
- State 0 if buyer has no unit of both categories.
- State 1 if buyer has 1 unit of food category and no unit of fire category.
- State 2 if unit on hand is reversed
- State 3 if buyer has a unit of both categories.
I will assert that the Buyer has a sigma-algebra. See Wikpedia Sigma-Algebra.
I'm going to assume that if the buyer is healthy he/she will be in state 3, else the buyer will be in state 0,1 or 2. I'm going to borrow a simple able-ill-death state model from
STOCHASTIC PROCESSES: LEARNING THE LANGUAGE
This very simple model implies that the probability of being in the "able" state is equal to the probability of being in state 3. I will build on this very simple model to obtain a realistic model of Society.
It can be seen that the buyer's state at a point in his/hers life is more complex than just previous shown. Examples: buyer does not use all of the fire category at warm climates and buyer may have guest that entails more food used.
A seller has a decision about his product. He wants to maximize his profit with very little effort. This can be illustrated as a Knapsack Problem. The buyer is also using the same decision making process. The seller can store his product and wait for pricing power. The buyer can use what's in his/her storage. Shelf life must also be considered by the buyer and seller.
Consumers/Firms try to forecast their future worth, but it is my opinion their ability to forecast is limited. I will assume the following are true:
- Debt levels can be forecast. Debt Payment = f(Payments at interest rate1, ..., Payments at interest rateN).
- Excess storage can lead to new investments.
Consumers/Firms make decisions based on current state and a future period based on current debt levels and future worth. Mathematically, they are sampling a value with a Dirac comb (See Wikpedia:Nyquist–Shannon sampling theorem). I will point out the fact that the Consumers'/Firms' decision produces the wave nature of consumption and production. Before I continue this section, a side trip is in order to get the form of the time component and the creation of wealth. This leads towards the topics of Natural, Creation and Annihilation Operators.
Natural, Creation and Annihilation Operators
I will assume the following for a simple model.
The returns to scale is represented by
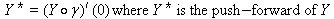

Consumers'/Firms' decisions on whether to store will determine future output. For simplicity, I will assume output Y has a covariant derivative. Y having a covariant derivative is to meet the requirement of the real world use of capital and labor from other markets. This implies the covariant derivative is on the mixed tensor from K space and its dual, L space. This restriction can be relaxed if capital and labor comes from the same market (Lie Derivative can be used).
Capital and Labor are equivalent, therefore, MONEY is given by a gauge covariant derivative.
My model will use a gauge and the gauge covariant derivative. This is to keep the model's analysis in line with Neoclassic Theories of cost and/or production functions that uses isoquants. In general, the curve used, in this general global economic theory, will not be like those from general relativity. The path a market takes can not be described like light passing by a gravitational field. This is due to the stochastic natural of the economic models.
As a side note: Consumers and Firms use data from their lives along with data given by statistical means. One can argue Consumers and Firms are acting on information that has some uncertainty. If one assumes output Y has canonical coordinates (Y has Y dot, where Y dot is a “momentum” of output Y) then one can come up with an argument about using the Hamilton form of gauge theory.
I need to change the definition of out Y. I will define the interaction of labor (from Labor space) with that from capital (from Capital space) as the process (a transformation). Neoclassical theory defines output minus consummation as savings(investments). I will keep this idea, but call it storage. Therefore, output is equal to the process plus storage. My definition requires output from storage needs to interact with the process to create new wealth. Example: keeping cash in the mattress creates no new wealth. Its value will be determined by inflation/deflation at time of use.
I will also assume there will be no discontinues. Example: It took time for the financial system to collapse after the Stock Market crash of 29.
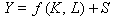
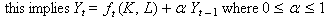
The above equation is not a working one. It shows that output, from time t – 1, was produced at a velocity of money, Vmoney(t – 1). This value, Vmoney(t), can be different when it is used at time t. This can be a source of sticky prices for the inventory.
The above equation can be forced into a form such as Total Energy = Kinetic Energy + Potential Energy by asserting that all new entries into the labor pool and new monies are placed into storage at t – 1 to be available for production at t. This implies produced labor, example robots, are not created. People, horses, etc... are created/dies which is the source of population growth/decline. New money is define as newly minted and printed money. Money, that accrue interest, is placed into the production side and then returned to storage.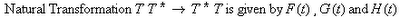
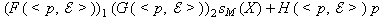
See Natural Operations in Differential Geometry pdf page 231 for proof.
There are many ways to solve the output equation. One way is to identify fundamental processes. Agriculture is broken down into energy used, transportation, distribution, etc... This way growing corn is the same as growing wheat. From this type of reasoning, a general linear group can be found to fit the problem. Such a route will remove the ET problem (trading fruit? for wheat).
Motivation for Constructing the Connection of Manifolds
One needs to look no further than the Neoclassical Theories for producers, consumers and growth. In general, none of these theories are gauge invariant. I will set my argument for the connection of manifolds by use of principle bundles by noting the topological properties of Neoclassical Theory. Note: I do not imply the existence of “space-time” coordinates, i.e. markets have space-time coordinates relating markets to geographic locations. Market manifolds have no relationship with respect to Earth coordinates.
See Wikipedia: Principal Bundle and Torsors Made Easy for background material.
Since there is an equivalent relationship between (co)tangent bundles and elasticity, it makes sense to designate elasticity as the fiber bundle. My assertion of the existence of “jet bundle” for global economic theory is correct (Neoclassical Theory does calculus on a manifold and is analytical). See Wikipedia: Fiber Bundle, Jet and Jet Bundle.
The function of the Fundamental Market is to prevent inelasticity to occur. The Fundamental Market acts as an infinite source. Inelasticity of “commodities” is due to the policies of government, consumer and producers behavior. This implies the “bare” topological interaction is between “production” and “consumption”. Government, consumer and producers behaviors, therefore, are intermediate processes that act on the “bare” interaction. My output equation is therefore the effect of the intermediate processes.
One does not have to rely on faith to understand the relationship between elasticity => K and L space. Solow’s model is the non-topological form of my output equation. It is helpful to use the Hamilton form of field theory to gain insight as to the relationship between elasticity and (K, L) space (generalize coordinates -> conical momentum).
The next major section will explain how economic data, futures, interest rate etc… can change can change the momentum of a market.
AND
What to do about derivates with respect to “velocities”: Economics deal with money and the velocity of money. The nominal exchange rate become the “filter” which allows the interaction of currencies between markets which in turn helps producers and consumers in their decisions about which “commodities” from which markets are used. The previous statement is the bad news. The good news is one can find a transformation of the frame of reference in which the derivate with respect to velocity can be set to zero. This property is due the markets are the same object, but in a different state.
Exchange of Money and Homotopy
First a simple example:
i) I have a penny and you have a penny. I ask you to exchange our pennies. By a simple definition: this exchange has a velocity component, however, this exchange has no effect on the market.
ii) If I were to say that you have a penny that I think has a value more than its representation, this exchange does affect the market.
Math speak:
X is a topological space with a point x(0) in that space. There exists continuous functions
f:[0, 1] -> X with the property f(0) = x(0) = f(1).
I am going to define (i) example as the map of simple connected parameterization functions with no other points in between. The significance of (i) can be seen if a central bank is substituted for you and I.
Examples: the Federal Reserve can represent “you” and “I”.
The Federal Reserve can represent “you” and the Bank of Japan as “I”.
ii) is an example of being path-connected.
A round trip of money, with respect to “I”, is homotopic with a round trip of money, with respect towards a central bank. A “loop” for a central bank has an equivalence relation with a “loop” for a consumer. A “loop” for a consumer has an equivalence relation with a “loop” for a firm. Same idea between firms and central banks.
The previous is the good news. An infinite number of loops/markets is the bad news.
One can assume that the aggregate of a society’s market as a path-connect loop exists. See Functions of Aggregates; What was that middle part again? This paper deals with aggregate price which is not guage invariant. Economist do not care if a loop exists. Economist concentrate on how it changes. One example of a path can be illustrated by a difference equation. See Poverty Trap.
In a simple sense; I’ll be taking a step back from the details. I will assert “Markets” have a simply-connected path -> No Holes. In other words; Doughnut<->Teacup topological space is not a “Market” space. I will also assert the same parameterization, that allows the invariant of homotopy, is good for the topological space to be path-connected.
Momentum of a Market
One must note the following observation: Consumers and firms may change the momentum of a market when they interact via the buying and selling of goods, service, and futures contracts etc.. They make borrowing/lending decisions based on current information and a prediction of their future financial state. In general, this old saying is true: “It’s not what you did for me today; it’s what you will do tomorrow”. Economic/policy decisions concentrate on what will happen in the future. Consumers/Firms/Investors make bets on the future. These bet may be correct, however, the act can change the momentum such that some may win, and some may lose. These interactions are dynamic probes that will change the state of the market.
The first item is the existence of a group structure and its algebra. In this case, the group structure is the Tangent Space, which is a Lie Group and its Lie Algebra. The Lie Group along with its Lie Algebra allows a trivial Tangent Bundle. TG -> G x g where G is the Lie Group and g is its algebra.
One more item can be proven, given the above relationship between Tangent Space G and g, is the fact that elasticity is also a Lie Group. This is due to its equivalent relationship to the Tangent Space. The result of this relationship is the exists of a trivial Elasticity Bundle. EG -> G x ge where EG is the Elasticity Space and ge its Lie Algebra. There exists a conical form of Elasticity Space (as there exists a conical form of Tangent Space G).
Dynamic Programming Revisited
Economists use the notion of equilibrium. This can be stated, using stochastic terms, by the following:
S is a state space with the set of distributions on S denoted by P(S).

A discrete stochastic kernel p is a function from S X S into [0, 1] with the property of p(x, y) greater than or equal to 0 for each (x, y) in S X S and
Equilibrium is defined by the idea of the stochastic kernel p contains the complete description of the dynamic model. This idea is fine in an isolated economy; however, there is no way to describe a global economy. In other words, market A is using output from market B with both markets acting independently with their own policies. A global market can be represented by:
One can interpret the convolution as a destruct of market A and the creation of two markets, one of which is use in the combine market along with the destruction of market B and the creation of two markets, one of which is used. The resulting model can go chaotic.
The creation (convolution)/annihilation (de-convolution) of a market M:
requires a linear transformation. A solution can be found if one restricts the topological properties of the underling system to have the following:
- The topological space X is a Hausdorff space. This makes X a metric space.
- A function h: X -> Y is a homeomorphism. X and Y are homeomorphic.
- I’m going to use compact Lie group. A Lie group makes the dynamic system easier to handle. This also makes the connection between differential manifold and stochastic system easier to analysis.

If A and B are two markets there exists a transformation such that:

This implies my state space to be the Elasticity space. The Elasticity space contains all of the information: consumers‘, firms’ and governments’ policies.
The "function" of Time
I want to begin this section by proving the existence of elasticity of labor with respect to capital. In previous entries I proved the existence of the “value added chain” as a topological lift between K(capital) vector(co-vector) space and L(labor) co-vector(vector) space. The K-L spaces are linear which implies there exists a Cartesian product of this multi-linear space:

This is a handy tensor because one can raise and lower indexes by the use of the metric tensor and a contraction (convert capital into labor and visa versa).
I’m going to use scalars to show the concept of the time evolution of the arc elasticity of labor with respect to capital (% change of labor with respect to the % change of capital).



The time evolution is the direct product of the arc elasticity of labor with respect to capital and the arc elasticity of time (its inverse; which implies none of the matrixes are singular).
It is realistic to simplify this time evolution to a set of average times. As time evolves in steps those shocks, that have a short period, affect the evolution before those with longer periods. In other words, the time evolution is a superposition of average periods.
Time evolution of an economy is model by the time evolution of Elasticity space. Financial companies have a way which makes them money. See Applied Mathematical Finance for quick info and other resources. Another analytical tool can be use, as exemplified by the infinite horizon Markov control process. The upshot of this line of thought: Risk and Reward are topological spaces.
A parameterize, continuous function of the form h(t, 0) = f(t), h(t, 1) = g(t) and h(0, t) = x(0) = h(1, t) where h[0, 1]. I will keep this simple and assume there is a fundamental group. If one attaches time to the parameter t, then the functions describes “products” of value with a velocity.Defining the interaction between those who need protection and those who are willing to take it as a transfer of value, implies the existence of at least one on each side of the trade (from the stand point of Homotopy there exist a self interaction which, by my definition, transfer no value).
PROOF:
f1, g1 : X -> Y are homotopic, and f2, g2 : Y -> Z are homotopic. Their composition f2 o f1 and g2 o g1 : X -Z are also homotopic. My working principle is to let X -> Y represent the transfer of value due to one side of the trade and Y -> Z represents the transfer of value due to the other side to produce the final product. Z represents the final output space for this example. Two different processes are represented by f’s and g’s (no self interaction). It is require that the “length” of the path in Z not be zero (no transfer of value with self interaction) and its length be the same for f‘s and g‘s. From an economic point of view the value of a product can be consider a constant for the period in question. End Points are fixed in Homotopy.
Let (S, L, u) be any measure space, let (S’, L’) be a measure space, let T:S -> S’ be a measure function and let

be the image measure of u under T. If w: S’ -> R is a measure function and either w is nonnegative or

is finite, then

where the first integral is over S’ and the second is over S. The idea here is that u will be some measure one is used to working with, such as Lebesgue measure, and u composite with the inverse of T is more complex.
Elasticity space is a compact Lie group which makes the Risk and Reward space a compact Lie group. The coordinate transformation is an equivalence relationship.
In general, if expectations are not meet, consumers‘, firms’ and governments’ expectations are also not meet. A “Restoring Force” develops such that Risk and Rewards are rebalanced.
In general, Elasticity Space needs e-algebra to reflect its dynamic properties. General Theory of Relativity uses surface geodesics as the shortest distance on a manifold. Einstein’s concept of matter telling space how to deform and space telling matter how to move is very useful for the following generalization to the “function” of time. Elasticity of Time generates the “economic” forces in markets.
An example of this economic force can be illustrated by Infinite horizon Markov control processes which are a class of high dimensional optimization problems; in fact the objective function is often defined over a space of infinite dimension. Actions taken by an agent affect the path of a state variable through time. Each control “policy” leads to a Markov process on the state space, and different processes give different levels of expected reward, or utility. Bounded horizon Markov control processes are uninteresting to economist because the constraints violate their economic models. I will concentrate on a solution that has been used for bounded processes: compact the state space, so that the necessarily continuous reward function is automatically bounded on the state (despite perhaps being unbounded on a larger domain). This can be done if one looks at embedded manifolds.
My thinking, of the above problem, as a physicist gives me insight as to the nature of time. It’s a transformation between time and the embedded manifolds(s). Firms, Consumers, Governments and their aggregate are on a market manifold whose dynamic evolution can be described by a parametric curve(s) in time (velocity of a market). At each point on the manifold there exists infinite many parameter curves (n-winding numbers). Each of these parameter curve is point on a tangent plane of an embedded manifold. Each point on the embedded manifold has an associated with an exponential map which describes its respected surface geodesic. The elasticity of time allows a smooth transformation between manifolds. This (embedded)manifold transformation gives rise the “force” of the market. In other words, markets can be describe as a closed system (no external stimuli needed). The topological lift due to Risk and Reward is controlled by firms, consumers, governments and their respected aggregate. Hence the duality between economic policies and government types.
A side note: All isomorphic and path connected systems have the elasticity space (these are a highly restrictive requirements that can be relaxed as the space is investigated). Einstein’s concept can have a force exerted by a change of mass due to the fact space will change (something physics can image on how this can be done). Another example can be illustrated by rotation of a point. This can be seen as a transformation of the (embedded)manifold. Hence a force due to this transformation. This is my answer to the General Theory - Angular Momentum problem.

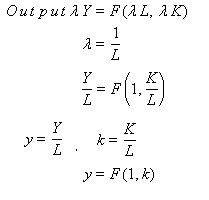

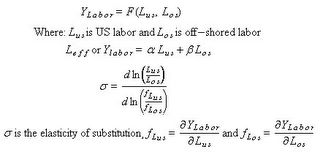
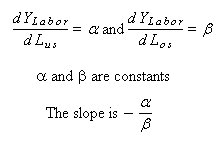
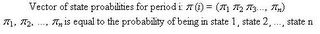

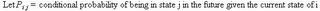
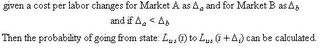


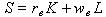
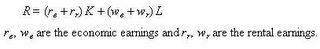

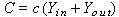
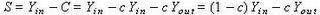
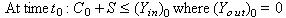

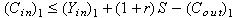








5 comments:
Interesting site. Useful information. Bookmarked.
»
I say briefly: Best! Useful information. Good job guys.
»
Amiable dispatch and this mail helped me alot in my college assignement. Say thank you you as your information.
Dear friends
We do not agree with this year BRITs 2010 decision.
Please go to see our little web survey
http://micropoll.com/t/KDqOnZBCWt
Lady Gaga can not be better than Nina Hagen
Poll supported by BRIT awards 2010 sponsor femmestyle
[url=http://www.femmestyle.ch/earcorrection.html]ohrenkorrektur[/url]
Do you have a burning question we could ask all the stars at The BRIT Awards?
start something with alesse facebook http://archive.org/details/seobinbila pilule contraceptive alesse effet secondaire [url=http://alessefl97.carbonmade.com/projects/4679945] alesse effets secondaires forum[/url] alesse 21 price canada mp3alese.comu alesse birth control reviews weight gain
mamoleptino321
edwards alessi price http://archive.org/details/studokcrapot alesse reviews 2012 [url=http://flavors.me/alesse_tempgestsagil1975] calesse wikipedia[/url] filme alese online.ro alesso years download mp3 skull alesse birth control cost canada
http://www.fiber-optic-transceiver-module.com/hp-transceiver-top-seller-this-week-hp-j9150a.html#comment-159153 http://cilgintalebeler.com/showthread.php?tid=33780 http://pabxbandung.com/pabx-bandung-panasonic-kx-tde200/pabx-bandung-panasonic-kx-tde200/comment-page-4/#comment-57431 http://www.icehill.rs/node/18#comment-44016 http://www.chanellro.com/viewthread.php?tid=3256809&extra=
start something with alesse contest http://flavors.me/alesse_taitalirect1983 buy alesse canada [url=http://archive.org/details/anmarusen] alesse birth control side effects[/url] alesse reviews side effects filmealese.ro 2011 filme alese.ro horror
Post a Comment